INVESTIGACIÓN DE OPERACIONES

 

Cuando no existe ningún punto del plano que satisfaga simultáneamente todas las restricciones, se considera que el problema:

a. no tendrá solución Respuesta Correcta

b. tiene múltiples soluciones

c. no una solución acotada

d. tienen una solución óptima

Pregunta 2

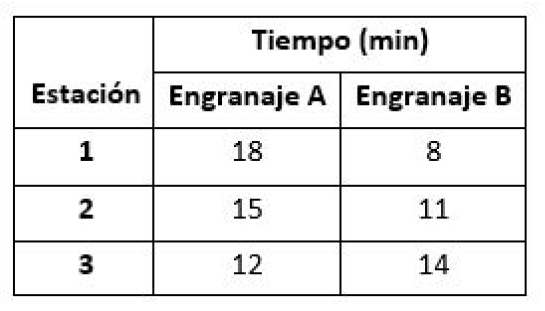
Un pequeño taller metalmecánico fabrica dos tipos de engranajes para una ensambladora automotriz. Para la fabricación de los engranajes la compañía cuenta con tres estaciones de trabajo y los tiempos de cada tipo de engranaje en cada estación se muestran en la tabla a continuación:

 

Finalmente, el taller trabaja 12 horas al día, pero se deben hacer mantenimientos diarios a cada estación, lo que consume 30 minutos de la estación uno, 45 minutos de la estación dos y 25 minutos de la estación tres.

Si el gerente de producción desea minimizar el tiempo muerto total de las tres estaciones y se plantea un modelo lineal para hallar la cantidad óptima de cada tipo de engranaje a fabricar, definiendo las variables de decisión como:

X: Cantidad de engranajes tipo A a fabricar

Y: Cantidad de engranajes tipo B a fabricar

¿Cuál sería la restricción asociada al tiempo disponible en la estación dos?

a. 15X + 11Y ≤ 675 Respuesta Correcta

b. 15X + 11Y ≤720

c. 15X + 11Y ≤ 12 d) 15X + 11Y ≥ 12

Pregunta 3

Un pequeño taller metalmecánico fabrica dos tipos de engranajes para una ensambladora automotriz. Para la fabricación de los engranajes la compañía cuenta con tres estaciones de trabajo y los tiempos de cada tipo de engranaje en cada estación se muestran en la tabla a continuación:

Finalmente, el taller trabaja 12 horas al día, pero se deben hacer mantenimientos diarios a cada estación, lo que consume 30 minutos de la estación uno, 45 minutos de la estación dos y 25 minutos de la estación tres.

Si el gerente de producción desea minimizar el tiempo muerto total de las tres estaciones y se plantea un modelo lineal para hallar la cantidad óptima de cada tipo de engranaje a fabricar, definiendo las variables de decisión como:

X: Cantidad de engranajes tipo A a fabricar

Y: Cantidad de engranajes tipo B a fabricar

¿Cuántos puntos extremos tiene la región factible del problema?

a. 5 Respuesta Correcta

b. 10

c. 4

d. 6

Pregunta 4

Cuando se formula un programa lineal es necesario verificar que tanto la función objetivo, como las restricciones cumplan con 

a. las cuatro hipótesis Respuesta Correcta

b. las variables de decisión

c. la función objetivo

d. los criterios lineales

Pregunta 5

Ecopetroleos es una empresa petrolera que tiene una refinería en la costa norte del país. La refinería procesa petróleo nacional e importado, produciendo gasolina, diésel, y lubricantes.

Los dos crudos se diferencian en su composición química, por lo que producen diferentes cantidades de cada producto como se muestra a continuación en la tabla:

Tipo de Petróleo	Producción (barriles)
	Gasolina	Diésel	Lubricantes
Nacional	0.35	0.4	0.15
Importado	0.4	0.15	0.35

El restante 10% del crudo, en los dos casos, se pierde en el proceso de refinación.

Los crudos también difieren en precio y disponibilidad. Ecopetroleos puede comprar hasta 15 000 barriles de crudo nacional por día a un precio de \$50 por barril. Por otra parte, puede comprar un máximo de 8000 barriles importados por día a un precio de \$55 por barril.

Los contratos establecidos por Ecopetroleos lo obligan a producir 3 000 barriles diarios de gasolina y 1 500 barriles diarios de lubricantes. Sin embargo, por legislación no puede producir más de 2 000 barriles diarios de diésel.

El gerente de la compañía desea saber cómo se pueden cumplir estos requerimientos al menor costo posible.

Si se plantea un modelo lineal, definiendo las variables de decisión como:

X: Cantidad de barriles de crudo nacional a comprar diariamente

Y: Cantidad de barriles de crudo importado a comprar diariamente

¿Cuál es la cantidad óptima de crudo nacional a comprar diariamente?

(Se redondearon los resultados a una cifra decimal)

a. 0.0 Respuesta Correcta

b. 3255.8

c. 5000.0

d. 15000.0

Pregunta 6

¿Qué tipo de solución se usa cuando una de las curvas de nivel de la función objetivo con el valor óptimo coincide con alguna de las restricciones que define alguna de las caras de la región factible?

a. Óptimos alternos Respuesta Correcta

b. Solución no acotada

c. Solución óptima única

d. Problema no factible

Pregunta 7

Ecopetroleos es una empresa petrolera que tiene una refinería en la costa norte del país. La refinería procesa petróleo nacional e importado, produciendo gasolina, diésel, y lubricantes.

Los dos crudos se diferencian en su composición química, por lo que producen diferentes cantidades de cada producto como se muestra a continuación en la tabla:

Tipo de Petróleo	Producción (barriles)
	Gasolina	Diésel	Lubricantes
Nacional	0.35	0.4	0.15
Importado	0.4	0.15	0.35

El restante 10% del crudo, en los dos casos, se pierde en el proceso de refinación.

Los crudos también difieren en precio y disponibilidad. Ecopetroleos puede comprar hasta 15 000 barriles de crudo nacional por día a un precio de \$50 por barril. Por otra parte, puede comprar un máximo de 8000 barriles importados por día a un precio de \$55 por barril.

Los contratos establecidos por Ecopetroleos lo obligan a producir 3 000 barriles diarios de gasolina y 1 500 barriles diarios de lubricantes. Sin embargo, por legislación no puede producir más de 2 000 barriles diarios de diésel.

El gerente de la compañía desea saber cómo se pueden cumplir estos requerimientos al menor costo posible.

Si se plantea un modelo lineal, definiendo las variables de decisión como:

X: Cantidad de barriles de crudo nacional a comprar diariamente

Y: Cantidad de barriles de crudo importado a comprar diariamente

¿Cuál sería la restricción asociada la producción de gasolina?

a. 0.35X + 0.40Y ≥ 3000 Respuesta Correcta

b. 0.35X + 0.40Y ≤ 3000

c. X + Y ≥ 3000

d. X + Y ≤ 3000

Pregunta 8

Las cuatro hipótesis de un programa lineal son:

a. Proporcionalidad, aditivitdad, divisibilidad y certidumbre. Respuesta Correcta

b. Restricciones, aditivitdad, divisibilidad y maximización.

c. Divisibilidad, aditivitdad, variables de decisión y certidumbre.

d. Maximización, optimización, criterios lineales y certidumbre.

Pregunta 9

¿Cuáles son los elementos de un modelo de programación lineal?

a. Función objetivo, criterio de optimización, variables de decisión y restricciones. Respuesta Correcta

b. Variables de decisión, función lineal, notación básica y criterio de optimización.

c. Proporcionalidad, función de restricciones, objetivos y criterios lineales.

d. Variables de optimización, límite superior, límite inferior y criterio de optimización.

Pregunta 10

¿Cuál de las siguientes expresiones representa una función lineal?

a. f (x) = 3x + 1 3

b. (x) = 5x + 1 2

c. f (xy) = 3x + 5y − 2 Respuesta Correcta

d. f (x) = √−x−−+−−1

Pregunta 11

Cual se las siguientes ecuaciones representan la forma general de una función lineal

a. y = mx + b Respuesta Correcta

b. y = mx + 2b 2

c. y = mx + b

d. √y = + x

Pregunta 12

Un pequeño taller metalmecánico fabrica dos tipos de engranajes para una ensambladora automotriz. Para la fabricación de los engranajes la compañía cuenta con tres estaciones de trabajo y los tiempos de cada tipo de engranaje en cada estación se muestran en la tabla a continuación:

Finalmente, el taller trabaja 12 horas al día, pero se deben hacer mantenimientos diarios a cada estación, lo que consume 30 minutos de la estación uno, 45 minutos de la estación dos y 25 minutos de la estación tres.

Si el gerente de producción desea minimizar el tiempo muerto total de las tres estaciones y se plantea un modelo lineal para hallar la cantidad óptima de cada tipo de engranaje a fabricar, definiendo las variables de decisión como:

X: Cantidad de engranajes tipo A a fabricar

Y: Cantidad de engranajes tipo B a fabricar

¿En cuál de los siguientes puntos se encuentra la solución óptima del problema? (Se redondearon los resultados a una cifra decimal)

a. (23.1, 29.8) Respuesta Correcta

b. (0.0, 61.4)

c. (38.3, 0.0)

d. (45.0, 0.0)

Pregunta 13

Un pequeño taller metalmecánico fabrica dos tipos de engranajes para una ensambladora automotriz. Para la fabricación de los engranajes la compañía cuenta con tres estaciones de trabajo y los tiempos de cada tipo de engranaje en cada estación se muestran en la tabla a continuación:

Finalmente, el taller trabaja 12 horas al día, pero se deben hacer mantenimientos diarios a cada estación, lo que consume 30 minutos de la estación uno, 45 minutos de la estación dos y 25 minutos de la estación tres.

Si el gerente de producción desea minimizar el tiempo muerto total de las tres estaciones y se plantea un modelo lineal para hallar la cantidad óptima de cada tipo de engranaje a fabricar, definiendo las variables de decisión como:

X: Cantidad de engranajes tipo A a fabricar

Y: Cantidad de engranajes tipo B a fabricar

Al resolver el problema se encuentra que el mismo:

a. Tiene óptimos alternos Respuesta Correcta

b. Tiene solución única

c. No tiene solución factible

d. Es no acotado

Pregunta 14

¿Cuál de las siguientes expresiones no representa una función lineal?

a. f (x) = 3x + 1

b. f (x,y) = 3x + y − 2xy Respuesta Correcta

c. f (y) = −5y + 12 − 3

d. f (x,y) = 3x + 5y − 2

Pregunta 15

Ecopetroleos es una empresa petrolera que tiene una refinería en la costa norte del país. La refinería procesa petróleo nacional e importado, produciendo gasolina, diésel, y lubricantes.

Los dos crudos se diferencian en su composición química, por lo que producen diferentes cantidades de cada producto como se muestra a continuación en la tabla:

Tipo de Petróleo	Producción (barriles)
	Gasolina	Diésel	Lubricantes
Nacional	0.35	0.4	0.15
Importado	0.4	0.15	0.35

El restante 10% del crudo, en los dos casos, se pierde en el proceso de refinación.

Los crudos también difieren en precio y disponibilidad. Ecopetroleos puede comprar hasta 15 000 barriles de crudo nacional por día a un precio de \$50 por barril. Por otra parte, puede comprar un máximo de 8 000 barriles importados por día a un precio de \$55 por barril.

Los contratos establecidos por Ecopetroleos lo obligan a producir 3 000 barriles diarios de gasolina y 1 500 barriles diarios de lubricantes. Sin embargo, por legislación no puede producir más de 2 000 barriles diarios de diésel.

El gerente de la compañía desea saber cómo se pueden cumplir estos requerimientos al menor costo posible.

Si se plantea un modelo lineal, definiendo las variables de decisión como:

X: Cantidad de barriles de crudo nacional a comprar diariamente

Y: Cantidad de barriles de crudo importado a comprar diariamente

¿Cuál sería la restricción asociada a la cantidad de crudo importado disponible diariamente?

a. Y ≤ 8000 Respuesta Correcta

b. Y ≥8000

c. 55Y ≥ 8000

d. 55Y ≤ 8000